Gradient Descent :

Finding a local minimum or maximum of a given function is done using the iterative first-order optimization process known as gradient descent (GD).

To minimize a cost/loss function, this technique is frequently used in machine learning (ML) and deep learning (DL) (e.g. in a linear regression).

The gradient descent algorithm may not always work. There are two distinct prerequisites. A function needs to:

• differentiable

• convex

 

Not all functions meet these requirements, but if a function is differentiable, it has a derivative for every point in its domain.

 

Some examples of Differentiable equations:

f(x) = x² = d(x)/dx = 2x

f(x) = 3sin(x) = d(x)/dx = 3cos(x)

f(x) = x³-5x = d(x)/dx = 3x²-5

 

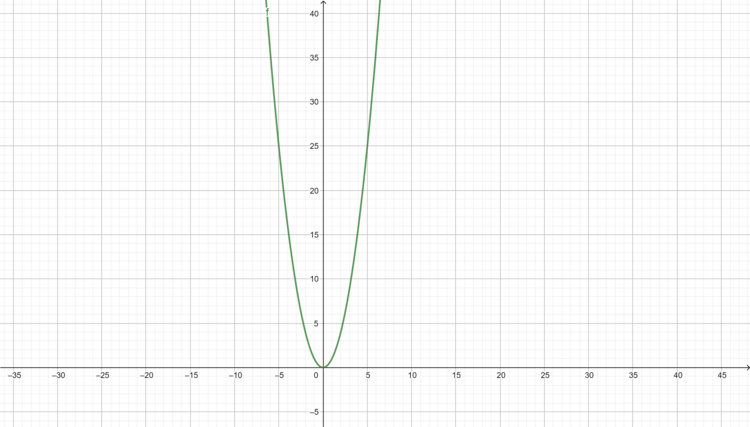
Figure E.1. f(x) = x² = d(x)/dx = 2x ; graphed equation

 

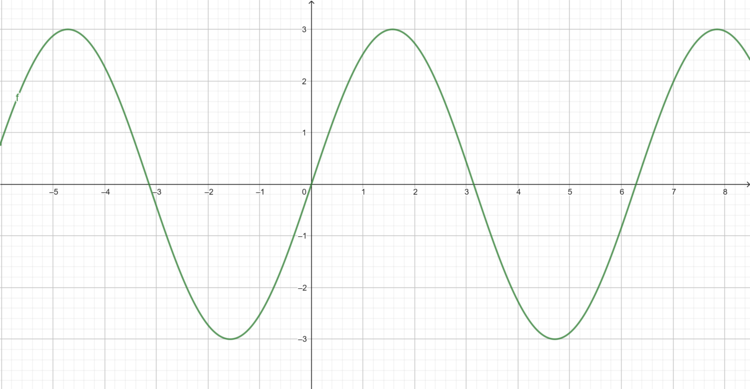
Figure E.2. f(x) = 3sin(x) = d(x)/dx = 3cos(x) ; graphed equation

 

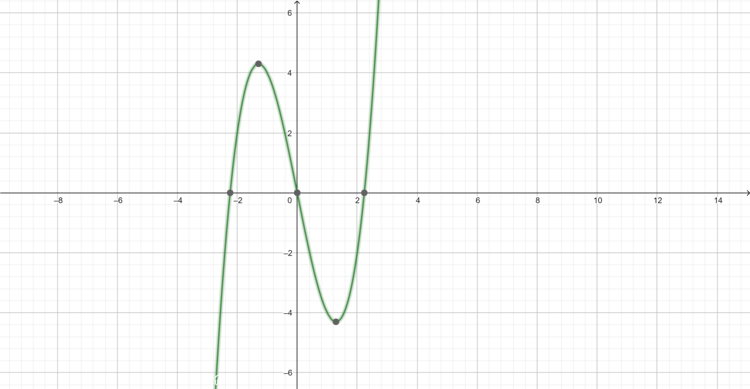
Figure E.3. f(x) = x³-5x = d(x)/dx = 3x²-5 ; graphed equation

 

Some non-differentiable equations are :

f(x) = x/|x|

f(x) = √|x|

f(x) = 1/x

 

Figure E.4. Some un-differentiable graphed equations.

 

A convex function is required.

This implies that the line segment joining the points of a univariate function lies on or above the curve rather than across it.

If it does, it has a local minimum rather than a global minimum.

Two functions with model section lines are shown below.

 

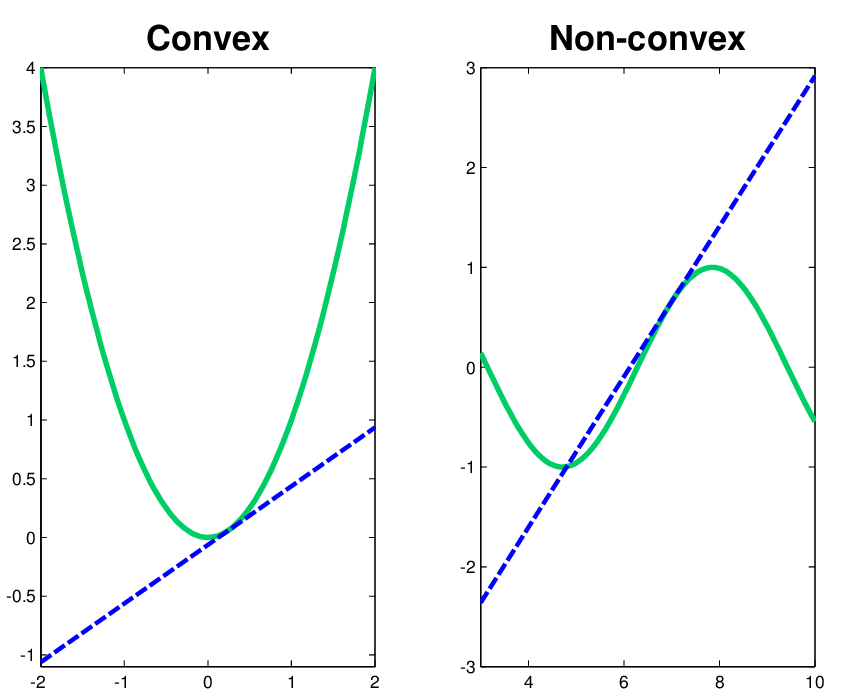
Figure E.5. Depiction of some Convex and non convex functions.

 

Lets get into some maths :

 

via GIPHY

 

Calculating the second derivative and determining whether or not its value is always greater than zero is another approach to quantitatively determine whether a univariate function is convex.

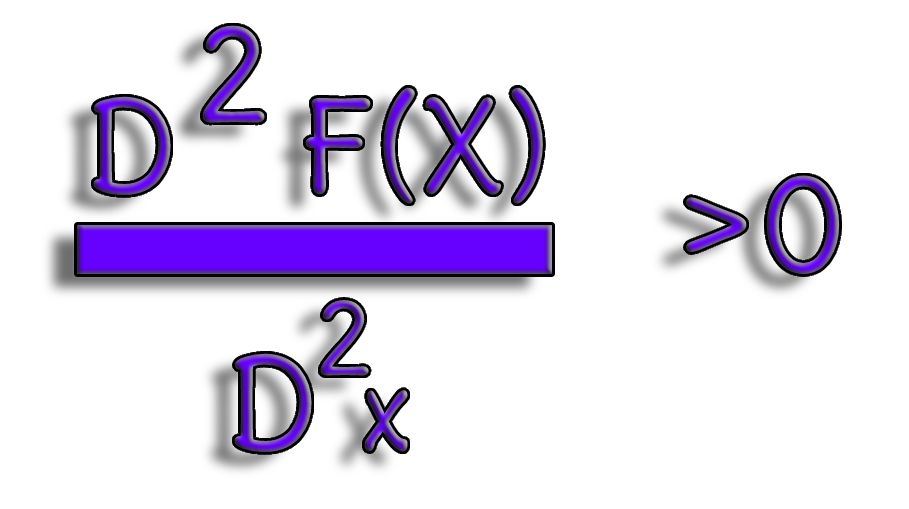
Figure E.6. Second order derivatives.

 

for x<0: function is convex

for 0<x<1: function is concave (the 2nd derivative < 0)

for x>1: function is convex again

 

>

 

 

Codeblock E.1. Standard Gradient Descent demonstration.

 

Download. Exam results csv file.

 

 

Codeblock E.2. Standard Gradient Descent demonstration with Exam result csv.

 

---- Summary ----

As of now you know all basics of Protein Structures.

• Linear regression

• Y=mx +b.

• intercept.

• Slope.

• etc..

Content

PythonPythonME

Introduction

Setting Up